Прогнозирование временных рядов нейронными сетями. Keras. Часть 1.

Продолжу рассматривать использование библиотеки Keras в решении задач различного рода. На этот раз рассмотрю, как работает прогнозирование временных рядов.

Разбираю код Дмитрия Романова, ведущего курс по нейронным сетям в «Университете Искуственного Интеллекта». Мой notebook с моделированием. Я немного оптимизировал код Дмитрия и добавил ряд пояснений, позволяющих разобраться в теме.

С временными рядами мы сталкиваемся повседневно. Это может быть описание каких-то природных событий, например, прогноз температуры, который жестко привязан к времени. Поменять местами последовательность нельзя, временной ряд рассыплется, если прогноз на 10-е поставить на 5-е число. Это будут совершенно другие данные. Т.е. делать перемешивание, как в случае, например, с определением авторства текстов, нельзя. К таким данным условно можно отнести многие, даже не представляющие собой зависимость именно от времени. Важно, что отсчеты нельзя менять местами. Например, аудиопоток, цены на акции, даже слова, поскольку изменить порядок букв в слове нельзя без искажения слова.

Обучающая выборка

Рассмотрим простой пример. Например, есть вектор, описывающий среднюю дневную температуру в течение 100 лет. Нужно построить прогноз на день вперед. Подготовим исходные данные для обучения сети.

• xTrainCount = 36500 отсчетов — длина вектора описывающего погоду за 100 лет * 365 дней.
• xLen = 100 — длина вектора xTrain.
• stepsForward = 1 — длина вектора yTrain или количество шагов (дней) на которое делается прогноз погоды.
• Shft = 1 — смещение вектора xLen относительно предыдущего. Обычно смещение делают на единицу.
• xCount = xTrainCount — xLen + 1 – stepsForward — количество строк в матрице, которое получится после «раскусывания» исходного временного ряда на xLen + stepsForward.
• Выборка xTrain — матрица с размерностью (xTrainCount — xLen + 1 – stepsForward, xLen).
• Выборка yTrain — матрица с размерностью (xTrainCount — xLen + 1 – stepsForward, stepsForward).
• Каждое значение yTrain — это значение температуры в некоторый день, но оно определяется температурой за предыдущие xLen дней. Нейронка пытается обобщить, как значение yTrain длиной stepsForward (предсказание на 1 или более дней) зависит от значений xTrain длиной xLen. Т.е. в какой-то степени yTrain = f(xTrain).
• При таком перемешивании мы как бы ставим задачу нейронной сети найти взаимосвязь последовательности длиной stepsForward (например, в случае прогноза погоды на 1 день) из значений в исходной выборке от предыдущих xLen значений (например, от 50 предыдущих дней).
• Если мы задаем поиск закономерностей между значением yTrain длиной stepsForward и остальными значениями, то в случае, когда stepsForward > 1, мы тренируем нейронную сеть на предсказание на несколько дней вперед.
• При наличии нейронной сети, предсказывающей на 1 день вперед, можно сделать предсказание на 2 и более дней, подавая на вход значение, предсказанное нейронной сетью ранее и убирая с начала по одному дню, чтобы длина вектора не изменилась. Однако, для такого варианта точность предсказания нейронкой на один день должна быть очень высокой, иначе прогноз быстро станет случайным.

Проверочная выборка

Важный вопрос, как формируется проверочная выборка. В случае с временными рядами все не так просто, как с некоторыми другими данными. В данном случае нельзя случайным образом выбрать, например, 20% данных из xTrain и yTrain.
P.S. Цифры на графике обозначают некоторую общность данных — это не данные выборок. Например, желтые — это вектора относящиеся к xTrain.

• Проверочная выборка берется из векторов xTrain и yTrain.
• Для проверочной выборки берется «хвост» данных длиной valLen.
• Данные для проверочной выборки берутся снизу (с конца), чтобы быть максимально близкими к прогнозным значениям. Скажем, в случае прогноза погоды если взять начало последовательности, то это будут данные столетней давности. За 100 лет ситуация с погодой могла измениться, поэтому использовать их для проверки неправильно.
• Между проверочной выборкой и обучающей нужно сделать промежуток длиной xLen + stepsForward. В этом промежутке данные xTrain и xVal в значительной степени пересекаются. Нейронка может «заучить» на обучающей выборке общие с проверочной выборкой паттерны. Это может обманчиво улучшить показатели на проверочной выборке. Поэтому приходится пожертвовать данными из этого промежутка — они исключаются из выборок.
• При коротких выборках, когда данных мало, можно исключать не диапазон xLen + stepsForward , а меньше, например, 80% от этой длины или менее. Это уже в значительной степени уменьшает взаимное перемешивание.

Прогнозирование акций Лукойл

В предыдущей статье по нейронным сетям я уже рассмотрел загрузку данных с ftp/http. В данном случае URL для загрузки данных:

filename = "onestock_oneminute.zip"

Загрузим данные из .csv с помощью Pandas. Нужно обратить внимание, что в качестве разделителя в csv используется «;» и в явном виде передать sep=’;’.

#Считываем данные с помощью pandas
base_data = pd.read_csv('18_19.csv', sep=';')
print(base_data.shape)

#Выводим пять первых строк
base_data.head()

         DATE      TIME    OPEN     MAX     MIN   CLOSE  VOLUME
0  03.01.2018  10:00:00  3341.0  3356.0  3340.0  3355.0    6088
1  03.01.2018  10:01:00  3355.0  3359.0  3353.0  3353.0    1624
2  03.01.2018  10:02:00  3351.5  3357.5  3351.5  3357.5     722
3  03.01.2018  10:03:00  3354.5  3360.0  3354.5  3358.0    3034
4  03.01.2018  10:04:00  3358.0  3360.0  3351.5  3360.0    1427

Что такое OHLC?

Видно, что показатели OHLC берутся с интервалом в 1 минуту.

OHLC – это сокращенное обозначение котировок, которые указываются для элементарной диаграммы ценового графика. В этой аббревиатуре :

• О обозначает Open – цену открытия интервала.
• H означает High (в нашем случае Max) — максимум цены интервала.
• L означает Low (Min) – минимум цены интервала.
• C означает Close – цену закрытия интервала.
• Volume — объем операций.

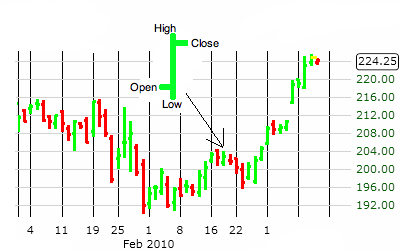
На графике OHLC каждый интервал времени (например, 5 минут) представлен OHLC ценами внутри этого интервала. OHLC — это один из основных показателей фьючерсной торговли на FOREX.

Подготовка данных

Для построения прогноза в данном случае не нужны колонки со временем и датой. Главное чтобы отсчеты брались через равные промежутки времени.

#Загружаем выборку и делаем предобработку, убрав две первые колонки
def getData(df):
  data = df
  return data.drop(columns=['DATE', 'TIME'], axis=1).astype(float)

#Получаем данные из файла
def getDataFromFile(fileName):
  df = pd.read_csv(fileName, sep=';') #Считываем файл с помощью pandas
  return getData(df) #Возвращаем считанные данные из файла

Файлы с данными по акциям идут по годам. Объединим два года для анализа.

#Считываем данные из двух файлов
#16-17 год и 18-19 год
data16_17 = getDataFromFile('16_17.csv')
data18_19 = getDataFromFile('18_19.csv')
print(data16_17.head(5))
print(data16_17.shape)

     OPEN     MAX     MIN   CLOSE  VOLUME
0  2351.0  2355.8  2350.0  2350.0  2547.0
1  2352.9  2355.7  2350.0  2355.7   195.0
2  2355.6  2356.0  2351.4  2354.1   257.0
3  2354.5  2355.0  2351.2  2353.7   763.0
4  2353.1  2353.9  2353.1  2353.6   231.0
(263925, 5)

#Объединяем базы из двух файлов
data = data16_17.append(data18_19)
print(data.head(5))
data = np.array(data) #Превращаем в numpy массив
print(data.shape)
print(max(data[:, 4]))

     OPEN     MAX     MIN   CLOSE  VOLUME
0  2351.0  2355.8  2350.0  2350.0  2547.0
1  2352.9  2355.7  2350.0  2355.7   195.0
2  2355.6  2356.0  2351.4  2354.1   257.0
3  2354.5  2355.0  2351.2  2353.7   763.0
4  2353.1  2353.9  2353.1  2353.6   231.0
(481872, 5)
4296341.0

#Сравниваем размеры
print(data16_17.shape) #Выводим размер первой базы
print(data18_19.shape) #Выводим размер второй базы
print(data.shape) #Выводим размер суммарной базы

(263925, 5)
(217947, 5)
(481872, 5)

Выведем данные OHLC на график:

#Отображаем исходные данные от точки start и длиной step
start = 0 #С какой точки начинаем
step = data.shape[0] #Сколько точек отрисуем

#Заполняем текстовые названия каналов данных
chanelNames = list(data16_17.columns) # ['Open', 'Max', 'Min', 'Close', 'Volume']

#Рисуем все графики данных
#Четыре основных канала - open, max, min, close
for i in range(4):
  #Отрисовываем часть данных
  #От начальной точки, до начальной точки + размер шага отрисовки
  plt.plot(data[start:start+step, i], 
          label=chanelNames[i])
plt.ylabel('Цена.руб')
plt.legend()
plt.show()

#Канал volume
plt.plot(data[start:start+step,4], label="Volume")
plt.legend()
plt.show()

Значения OHLC достаточно близки друг к другу, поэтому слились на первом графике.

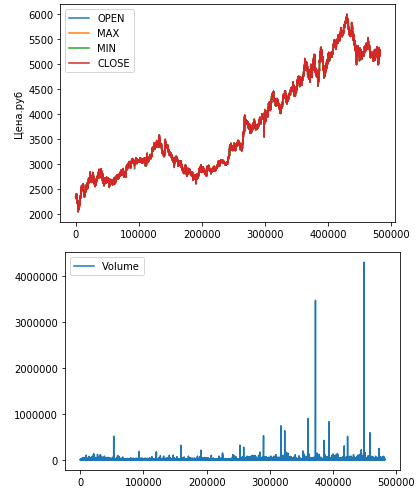
На втором графике видны два аномально высоких значения операций.

Проверка алгоритма подготовки данных

Смоделируем работу алгоритма по «раскусыванию» временного ряда на составляющие. Сгененирую простую последовательность, чтобы удобно ориентироваться в работе кода:

num = 20 
xData = np.arange(0, num).reshape(num,1)

print(xData)
stepsForward = 1
xLen = 5
xChannels = 0
print("xData.shape", xData.shape)
print("Range:", xData.shape[0] - xLen + 1 - stepsForward)

[[ 0]
 [ 1]
 [ 2]
 [ 3]
 [ 4]
 [ 5]
 [ 6]
 [ 7]
 [ 8]
 [ 9]
 [10]
 [11]
 [12]
 [13]
 [14]
 [15]
 [16]
 [17]
 [18]
 [19]]
xData.shape (20, 1)
Range: 15

Исходную последователность преобразуем в массив «раскусыванием»:

xTrain = np.array([xData[i:i + xLen, xChannels] for i in range(xData.shape[0] - xLen + 1 - stepsForward)])
print("xTrain.shape:", xTrain.shape)
print("xTrain:\r\n", xTrain)

xTrain.shape: (15, 5)
xTrain:
 [[ 0  1  2  3  4]
 [ 1  2  3  4  5]
 [ 2  3  4  5  6]
 [ 3  4  5  6  7]
 [ 4  5  6  7  8]
 [ 5  6  7  8  9]
 [ 6  7  8  9 10]
 [ 7  8  9 10 11]
 [ 8  9 10 11 12]
 [ 9 10 11 12 13]
 [10 11 12 13 14]
 [11 12 13 14 15]
 [12 13 14 15 16]
 [13 14 15 16 17]
 [14 15 16 17 18]]

Для получения yTrain нужно в каждой строке брать вектор длиной stepsForward, начиная с xLen, поскольку последовательность до xLen пошла в xTrain. Соотвественно, range начнется с xLen.

yChannels = [0]
yData = xData
if (stepsForward > 1):
  yTrain = np.array([yData[i:i + stepsForward, yChannels] for i in range(xLen, yData.shape[0] + 1 - stepsForward)])
else:
  yTrain = np.array([yData[i, yChannels] for i in range(xLen, yData.shape[0] + 1 - stepsForward)])

print("yTrain.shape", yTrain.shape)
print("yTrain:\r\n", y)  

yTrain.shape (15, 1)
yTrain:
 [[ 5]
 [ 6]
 [ 7]
 [ 8]
 [ 9]
 [10]
 [11]
 [12]
 [13]
 [14]
 [15]
 [16]
 [17]
 [18]
 [19]]

Видно, что значения вектора yTrain начинаются с xLen. Каждый элемент длиной stepsForward = 1. По сути, нейронка ищет закономерность между каждым yTrain и предыдущими xLen значений xTrain.

После получения исходной последовательности нужно разрезать массив на две части: обучающую выборку и валидационную. Кроме того между ними нужно выбросить «прослойку» размером bias записей. Это важно, чтобы гарантированно исключить перемешивание, т.е. чтобы в валидационную выборку не попали значения из обучающей.

В следюущей статье я сделал другой вариант разбивки на обучающую и проверочную выборку, он компактнее и понятнее.

valLen = 3

#Расчитываем отступ между обучающими о проверочными данными,  чтобы они не смешивались
xTrainLen = xTrain.shape[0]
bias = xLen + stepsForward + 2 #Выбрасываем bias записей. Небольшой резерв на 2 записи
print("xTrainLen:", xTrainLen)
print("bias:", bias)

#Берём из конечной части xTrain проверочную выборку
xVal = xTrain[xTrainLen-valLen:]
yVal = yTrain[xTrainLen-valLen:]
  
print("xVal:\r\n", xVal)
print("yVal:\r\n", yVal)

После запуска «раскусывалки» получим следующее:

xTrainLen: 15
bias: 8
xVal:
 [[12 13 14 15 16]
 [13 14 15 16 17]
 [14 15 16 17 18]]
yVal:
 [[17]
 [18]
 [19]]

• 3 записи остались для для проверочной выборки.
• 8 записей были выброшены (bias)
• 4 записи с начала оставлись для обучающей выборки

итого 15 записей.

#Оставшуюся часть используем под обучающую выборку
xTrain1 = xTrain[:xTrainLen-valLen-bias]
yTrain1 = yTrain[:xTrainLen-valLen-bias]

print("xTrain:\r\n", xTrain1)
print("yTrain:\r\n", yTrain1)

xTrain:
 [[0 1 2 3 4]
 [1 2 3 4 5]
 [2 3 4 5 6]
 [3 4 5 6 7]]
yTrain:
 [[5]
 [6]
 [7]
 [8]]

Код подготовки данных для временного ряда

#data - Numpy array
def DataNormalization(data, Channels, Normalization):
  #Выбираем тип нормализации x
  #0 - нормальное распределение
  #1 - нормирование до отрезка 0-1
  if (Normalization == 0):
    scaler = StandardScaler()
  else:
    scaler = MinMaxScaler()
  
  #Берём только те каналы, которые указаны в аргументе функции
  resData = data[:,Channels]

  if (len(resData.shape) == 1): #Если размерность входного массива - одномерный вектор, 
    print("Add one dimension")
    resData = np.expand_dims(resData, axis=1) #то добавляем размерность
  #Обучаем нормировщик
  scaler.fit(resData)
  #Нормируем данные
  resData = scaler.transform(resData)
  return (resData, scaler)

#Функция "раскусывания" данных для временных рядов
#data - данные
#xLen - размер фрема, по которому предсказываем
#xChannels - лист, номера каналов, по которым делаем анализ
#yChannels - лист, номера каналов, которые предсказываем
#stepsForward - на сколько шагов предсказываем в будущее
#если 1 - то на 1 шаг, можно использовать только при одном канале, указанном в yChannels
#xNormalization - нормализация входных каналов, 0 - нормальное распределение, 1 - к отрезку [0;1]
#yNormalization - нормализация прогнозируемых каналов, 0 - нормальное распределение, 1 - к отрезку [0;1]
#returnFlatten - делать ли одномерный вектор на выходе для Dense сетей
#valLen - сколько примеров брать для проверочной выборки (количество для обучающей посчитается автоматиески)
#convertToDerivative - bool, преобразовывали ли входные сигналы в производнуюa
def getXTrainFromTimeSeries(data, xLen, xChannels, yChannels, stepsForward, xNormalization, yNormalization, returnFlatten, valLen, convertToDerivative):
  
  #Если указано превращение данных в производную
  #То вычитаем поточечно из текущей точки предыдущую
  if (convertToDerivative):
    data = np.array([(d[1:]-d[:-1]) for d in data.T]).copy().T
  
  #Нормализуем x
  (xData, xScaler) = DataNormalization(data, xChannels, xNormalization)

  #Нормализуем y
  (yData, yScaler) = DataNormalization(data, yChannels, yNormalization)

  #Формируем xTrain
  #Раскусываем исходный ряд на куски xLen с шагом в 1
  xTrain = np.array([xData[i:i + xLen, xChannels] for i in range(xData.shape[0] - xLen + 1 - stepsForward)])
  
  #Формируем yTrain
  #Берём stepsForward шагов после завершения текущего x
  if (stepsForward > 1):
    yTrain = np.array([yData[i:i + stepsForward, yChannels] for i in range(xLen, yData.shape[0] + 1 - stepsForward)])
  else:
    yTrain = np.array([yData[i, yChannels] for i in range(xLen, yData.shape[0] + 1 - stepsForward)])

  #Расчитываем отступ между обучающими о проверочными данными
  #Чтобы они не смешивались
  xTrainLen = xTrain.shape[0]
  bias = xLen + stepsForward + 2

  #Берём из конечной части xTrain проверочную выборку
  xVal = xTrain[xTrainLen-valLen:]
  yVal = yTrain[xTrainLen-valLen:]
  
  #Оставшуюся часть используем под обучающую выборку
  xTrain = xTrain[:xTrainLen-valLen-bias]
  yTrain = yTrain[:xTrainLen-valLen-bias]

  #Если в функцию передали вернуть flatten сигнал (для Dense сети)
  #xTrain и xVal превращаем в flatten
  if (returnFlatten > 0):
    xTrain = np.array([x.flatten() for x in xTrain])
    xVal = np.array([x.flatten() for x in xVal])

  return (xTrain, yTrain), (xVal, yVal), (xScaler, yScaler)

Одномерная свертка

Забегая вперед скажу, что на этом временном ряде наилучшие показатели обеспечила одномерная свертка.

#Формируем параметры загрузки данных
xLen = 300
stepsForward = 1
xChannels = range(data.shape[1])
yChannels = [0]
xNormalization = 0
yNormalization = 0
valLen = 30000
returnFlatten = 0 #Возвращаем двумерные данные для свёртки
convertToDerivative = 0

#Загружаем данные
(xTrain, yTrain), (xVal, yVal), (xScaler, yScaler) = getXTrainFromTimeSeries(data, xLen, xChannels, yChannels, stepsForward, xNormalization, yNormalization, returnFlatten, valLen, convertToDerivative)

#Выводим размеры данных для проверки
print(xTrain.shape)
print(yTrain.shape)
print(xVal.shape)
print(yVal.shape)

(451269, 1500)
(451269, 1)
(30000, 1500)
(30000, 1)

modelC = Sequential()

modelC.add(Conv1D(50, 5, input_shape = (xTrain.shape[1], xTrain.shape[2]), activation="linear"))
modelC.add(Flatten())
modelC.add(Dense(10, activation="linear"))
modelC.add(Dense(yTrain.shape[1], activation="linear"))

modelC.compile(loss="mse", optimizer=Adam(lr=1e-4))

history = modelC.fit(xTrain, 
                    yTrain, 
                    epochs=20, 
                    batch_size=20, 
                    verbose=1,
                    validation_data=(xVal, yVal))

plt.plot(history.history['loss'], 
         label='Средняя абсолютная ошибка на обучающем наборе')
plt.plot(history.history['val_loss'], 
         label='Средняя абсолютная ошибка на проверочном наборе')
plt.ylabel('Средняя ошибка')
plt.legend()
plt.show()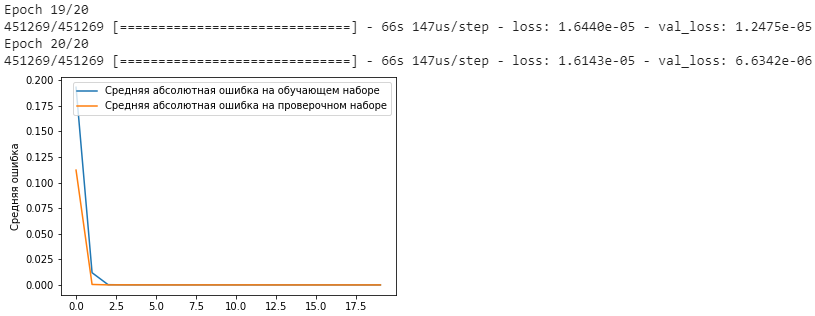

Визуализация результатов

#Функция рассчитываем результаты прогнозирования сети
#В аргументы принимает сеть (currModel) и проверочную выборку
#Выдаёт результаты предсказания predVal
#И правильные ответы в исходной размерности yValUnscaled (какими они были до нормирования)
def getPred(currModel, xVal, yVal, yScaler):
  #Предсказываем ответ сети по проверочной выборке
  #И возвращаем исходны масштаб данных, до нормализации
  predVal = yScaler.inverse_transform(currModel.predict(xVal))
  yValUnscaled = yScaler.inverse_transform(yVal)
  
  return (predVal, yValUnscaled)

#Функция расёта корреляции дух одномерных векторов
def correlate(a, b):
  return np.corrcoef(a, b)[0, 1] 

#Функция визуализирует графики, что предсказала сеть и какие были правильные ответы
#start - точка с которой начинаем отрисовку графика
#step - длина графика, которую отрисовываем
#channel - какой канал отрисовываем
def showPredict(start, step, channel, predVal, yValUnscaled):
  plt.plot(predVal[start:start+step, channel], 
           label='Прогноз')
  plt.plot(yValUnscaled[start:start+step, channel], 
           label='Базовый ряд')
  plt.xlabel('Время')
  plt.ylabel('Значение Close')
  plt.legend()
  plt.show()
  
#Функция рисуем корреляцию прогнозированного сигнала с правильным
#Смещая на различное количество шагов назад
#Для проверки появления эффекта автокорреляции
#channels - по каким каналам отображать корреляцию
#corrSteps - на какое количество шагов смещать сигнал назад для рассчёта корреляции
def showCorr(channels, corrSteps, predVal, yValUnscaled):
  #Проходим по всем каналам
  for ch in channels:
    corr = [] #Создаём пустой лист, в нём будут корреляции при смезении на i рагов обратно
    yLen = yValUnscaled.shape[0] #Запоминаем размер проверочной выборки

    #Постепенно увеличикаем шаг, насколько смещаем сигнал для проверки автокорреляции
    for i in range(corrSteps):
      #Получаем сигнал, смещённый на i шагов назад
      #predVal[i:, ch]
      #Сравниваем его с верными ответами, без смещения назад
      #yValUnscaled[:yLen-i,ch]
      #Рассчитываем их корреляцию и добавляем в лист
      corr.append(correlate(yValUnscaled[:yLen-i,ch], predVal[i:, ch]))

    #Отображаем график коррелций для данного шага
    plt.plot(corr, label='предсказание на ' + str(ch+1) + ' шаг')

  plt.xlabel('Время')
  plt.ylabel('Значение')
  plt.legend()
  plt.show()

#Прогнозируем данные текущей сетью
currModel = modelC
(predVal, yValUnscaled) = getPred(currModel, xVal, yVal, yScaler)

import matplotlib

matplotlib.style.use('ggplot')

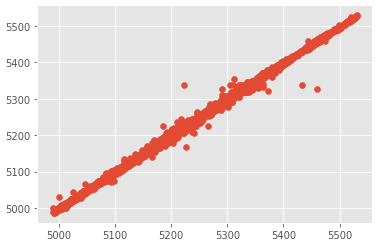
plt.scatter(predVal, yValUnscaled)
plt.show()

#Отображаем графики
showPredict(10000, 400, 0, predVal, yValUnscaled)

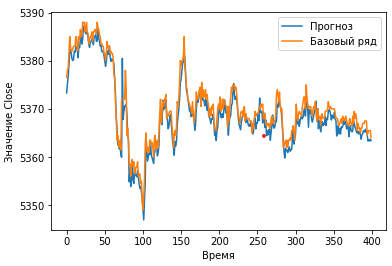
#Отображаем корреляцию
showCorr([0], 10, predVal, yValUnscaled)

Продолжение следует…

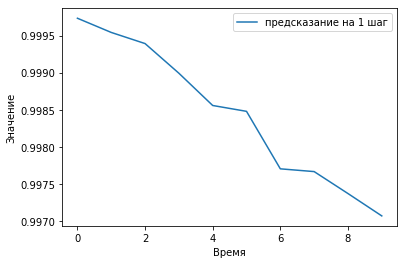
Полезные ссылки

• https://machinelearningmastery.com/how-to-develop-convolutional-neural-network-models-for-time-series-forecasting/
• https://machinelearningmastery.com/how-to-use-the-timeseriesgenerator-for-time-series-forecasting-in-keras/ — класс Keras TimeSeriesGenerator реализующий подготовку данных для прогнозирования временного ряда.