«Перевариваю» лекцию Дмитрием Романовым по регрессии из курса «Нейронные сети на Python» читаемого в «Университете искуственного интеллекта«.
Задача прогнозирования данных по известным цифровым рядам решалась с помощью различных методов регрессионного анализа. Чтобы сделать качественный прогноз приходилось использовать различные варианты уравнений регрессии, брать преобразование Фурье для выявления сезонной составляющей и использовать другие математические методы. При достаточном упорстве аналитика можно было найти комбинацию матметодов, неплохо предсказывающих поведение анализируемого параметра. Включение в модель категориальных данных было уже непросто, а текстовые — это вообще отдельная сложная тема.
Решение задачи регрессии с помощью нейронных сетей — иной подход. Рассмотрим его подробнее для начала на примере определения стоимости недвижимости из набора данных Boston Housing, включенном в Keras. Это 13 столбцов различных параметров описывающих недвижимость и всего-то 400 записей с информацией. Т.е. речь не идет о тысячах выборок для тренировки нейронки. Мой notebook после анализа лекции Дмитрия с экспериментами.
Подготовка данных
from tensorflow.keras.datasets import boston_housing from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense import matplotlib.pyplot as plt import numpy as np %matplotlib inline (x_train, y_train), (x_test, y_test) = boston_housing.load_data() #загрузка данных
Я буду рассматривать всю подготовительную фазу достаточно подробно, чтобы исключить любые вопросы, которые возникали у меня в ходе изучения кода. Заодно вспомним как работать с Python. 🙂
Итак, для начала нужно сделать нормализацию данных. В некоторых случаях нормализация позволяет существенно улучшить качество предсказания результатов сетью. Но, как говорит Дмитрий, «все гипотезы нужно тестировать». 🙂
Остановлюсь немного подробнее на нормализации в варианте Python. Для начала найдем среднее арифметическое (mean) на тестовом примере, чтобы лучше понять, как работают матричные операции Python.
value = [[x for x in range(0,5)],
[x for x in range(10,15)],
[x for x in range(20,25)]]
value = np.array(value)
print("Numpy array:", value)
sum = value.sum(axis=0)
print("Mean:", sum / value.shape[0]) Сначала суммируем по строкам. Для этого указываем axis=0. Если указать axis = 1, то суммирование будет проходить по столбцам, а это нам не нужно. После того, как просуммировали, делим на общее количество записей, которое получаем через: value.shape[0].
Numpy array: [[ 0 1 2 3 4] [10 11 12 13 14] [20 21 22 23 24]] Mean: [10. 11. 12. 13. 14.]
В numpy array есть стандартный метод для определения среднего арифметического «mean»:
mean = value.mean(axis=0) #Вычисляем среднее по строкам
print("Mean:\r\n", mean)
Mean:
[10. 11. 12. 13. 14.]При нормировке среднее арифметическое вычитается из исходных данных, чтобы новые значения лежали равномернее относительно оси х.
mean = x_train.mean(axis=0) x_train -= mean
Далее распространено деление полученных данных на стандартное отклонение. Явно выраженного физического смысла в этой процедуре нет. Однако, как указывается в источниках, приближая значения данных к диапазону функций активации, ускоряется корректировка весов и сеть быстрее сходится. Подробное описание можно посмотреть здесь.
std = x_train.std(axis=0) x_train /= std
Поскольку нормализацию нужно проделать и для обучающей x_train и для проверочной x_test выборки, воспользуемся функцией.
def norm(x): return (x - mean) / std x_train = norm(x_train); x_test = norm(x_test);
Поскольку функция активации sigmoid на выходе работает от 0 до 1, то сделаем нормировку для правильных ответов y_train. Для этого опустим минимальные значения к 0, вычтя из данных минимальное значение обучающей выборки.
Чтобы привести величины в выборке к 1, разделим данные на значение амплитуды взятое от новой (смещенной) выборки. Сохраняем минимальные и максимальные значения, поскольку после получения результатов на выходе сети нужно будет выполнить обратную процедуру.
При корректировке данных тестовой выборки воспользуемся полученным максимальным значением амплитуды от обучающей выборки:
# Приводим значения ответов в диапазон от 0 до 1 min_y = y_train.min() y_train = y_train - min_y #смещаем ответы к 0, вычитая минимальное значение max_y = y_train.max() #берем максимум от уже "опущенных" вниз на min_y данных y_train /= max_y #приводим к 1 обучающую выборку #нормируем ответы проверочной выборки, используя статистику min_y и max_y обучающей y_test = y_test - min_y y_test /= max_y
Предыдущий код можно написать по-другому, сместив на min_y и значения выборки, и значение максимума.
# Приводим значения ответов в диапазон от 0 до 1 min_y = y_train.min() max_y = y_train.max() - min_y #"опустим" максимум на min_y y_train = (y_train - min_y) / max_y #отклонение от минимума к амплитуде y_test = (y_test - min_y) / max_y
Остановлюсь чуть подробнее на моменте, что и обучающая, и проверочная выборка нормируется статистикой, полученной по обучающей выборке. Это сделано намеренно. В тексте статьи про регрессию есть небольшое пояснение почему так делается.
Использование статистики обучающей выборки при нормализации тестовой позволяет выявлять ошибки тестовой выборки, если её статистика отличается от обучающей. Скажем, в предыдущей статье по распознаванию автора книги я брал для тренировки сети первый том автора, а в качестве тестовой использовал второй.
После тренировки сети на обучающей выборке её веса будут подобраны таким образом, чтобы минимизировать ошибку. Сеть настроена на статистику обучающей выборки. Затем на сеть подается проверочная выборка, отнормированная статистикой обучающей. Сеть выдаст на выходе некоторый результат, который будет денормализован опять же с использованием статистики обучающей выборки. Если данные в проверочной выборке отличаются, то денормализация статистикой обучающей выборки приведет к росту ошибки.
Особенно явно рост ошибки может проявиться при использовании активационных функций, ограничивающих предельные значения на выходе нейронной сети. Например, в случае сигмоида возможные значения должны быть в коридоре: 0 — 1. Если после денормализации сеть предскажет значение большее 1 или меньшее 0, то оно будет усечено до 1 или 0 соответственно.
Нейронная сеть
Строим простую полносвязную нейронную сеть (feed forward neural network). Выходной слой с одним линейным нейроном — для задачи регрессии. Функция активации — RELU в промежуточном слое и sigmoid в выходном. Конфигурация сети взята из хорошего примера — https://www.tensorflow.org/tutorials/keras/basic_regression
model = Sequential() model.add(Dense(64, activation='relu', input_shape=(x_train.shape[1],))) model.add(Dense(64, activation='relu')) model.add(Dense(1, activation='sigmoid')) # sigmoid, т.к. данные от 0 до 1
Чтобы посмотреть архитектуру нейронной сети:
print(model.summary()) # архитектура нашей модели Model: "sequential_2" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_6 (Dense) (None, 64) 896 _________________________________________________________________ dense_7 (Dense) (None, 64) 4160 _________________________________________________________________ dense_8 (Dense) (None, 1) 65 ================================================================= Total params: 5,121 Trainable params: 5,121 Non-trainable params: 0
Компилируем сеть
# Т.к. задача регрессии, удобнее использовать mean square error(средне-квадратичная ошибка). # В качестве метрики берем mean absolute error (средний модуль ошибки) model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
И обучаем:
history = model.fit(x_train,
y_train,
epochs=100,
validation_split=0.1,
verbose=2)Делаем прогноз, приведя полученные значения ответов сети к нашим значениям, умножив на max_y (приводим амплитуду к нормальному виду) и «подняв» на min_y:
# Делаем прогноз. Возвращается копия предсказания в виде одномерного массива pred = model.predict(x_test).flatten() # Возвращаем к прежнему размеру pred = pred * max_y + min_y y_test = y_test * max_y + min_y
Проверяем, какая ошибка (средний модуль отклонения) получилась:
# Средний модуль отклонения err = np.mean(abs(pred - y_test)) print(err) 2.678478168038761
И получаем довольно хорошую ошибку при том, что вся процедура подбора модели предсказания прошла без нашего участия. В случае с классической регрессией пришлось бы посидеть немало времени, чтобы сделать необходимые преобразования исходных данных, которые можно было бы использовать для построения функции регрессии. Но в этом случае бонусом было бы то, что мы смогли бы увидеть полученную функцию. В случае нейронки полученная модель — «черный ящик».
# Средняя цена по выборке print(np.mean(y_test)) 23.07843137254902
Если построить результаты предсказания сетью значений, то можно заметить, что без шаманства с архитектурой нейронной сети, очистки входных данных и пр. качество предсказания довольно неплохое:
# Предсказание vs правильный ответ
for i in range(len(pred)):
print("Сеть сказала: ", round(pred[i],2), ", а верный ответ: ", round(y_test[i],2), ", разница: ", round(pred[i] - y_test[i],2))
Сеть сказала: 9.68 , а верный ответ: 7.2 , разница: 2.48
Сеть сказала: 18.21 , а верный ответ: 18.8 , разница: -0.59
Сеть сказала: 21.38 , а верный ответ: 19.0 , разница: 2.38
Сеть сказала: 36.57 , а верный ответ: 27.0 , разница: 9.57
Сеть сказала: 26.3 , а верный ответ: 22.2 , разница: 4.1
Сеть сказала: 24.11 , а верный ответ: 24.5 , разница: -0.39Естественно, для каких-то входных данных ошибка значительна, но, вполне вероятно, что в данных есть аномалии. Этот момент нужно изучать дополнительно.
Визуализируем полученные данные:
# Считаем графики ошибки
plt.plot(history.history['mean_absolute_error'],
label='Средняя абсолютная ошибка на обучающем наборе')
plt.plot(history.history['val_mean_absolute_error'],
label='Средняя абсолютная ошибка на проверочном наборе')
plt.xlabel('Эпоха обучения')
plt.ylabel('Средняя абсолютная ошибка')
plt.legend()
plt.show()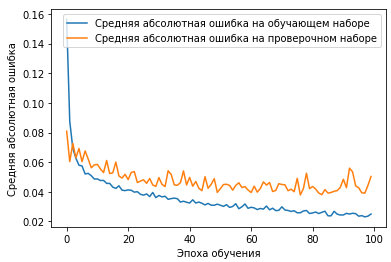
# Разброс предсказаний может показать перекос, если есть
plt.scatter(y_test, pred)
plt.xlabel('Правильные значение, $1K')
plt.ylabel('Предсказания, $1K')
plt.axis('equal')
plt.xlim(plt.xlim())
plt.ylim(plt.ylim())
plt.plot([-100, 100], [-100, 100])
plt.show()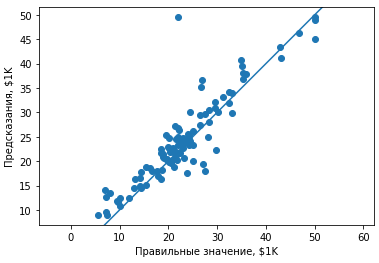
Видно, что результаты предсказания довольно неплохо укладываются относительно верных результатов за исключением одного выброса. Скорее всего в исходных данных для этого значения будут какие-то значительные аномалии, которые позволят сделать вычистку данных.
Гистограмма ошибок следующая:
#Разность предсказанного и правильного ответа
error = pred - y_test
#Построение гистограммы
plt.hist(abs(error), bins = 25)
plt.xlabel("Значение ошибки, $1K")
plt.ylabel("Количество")
plt.show()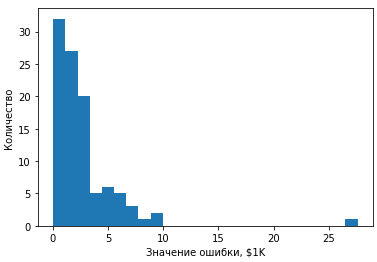
Видно, что большая часть ошибок укладывается в диапазон примерно до 4000$, и единственный аномальный вариант — с ошибкой в районе 27 тыс. $ Понятно, что в реальной жизни при выполнении прогноза сравнивать будет не с чем, поэтому нужно будет выработать критерии для идентификации явно аномальных значений в предсказании.
Полезные ссылки
- Прогнозирование финансовых временных рядов с MLP в Keras — https://webhamster.ru/mytetrashare/index/mtb0/1539612644nodqf6fjw9
- Deep learning: the final frontier for signal processing and time series analysis? — https://medium.com/@alexrachnog/deep-learning-the-final-frontier-for-signal-processing-and-time-series-analysis-734307167ad6
- A Guide For Time Series Prediction Using Recurrent Neural Networks (LSTMs) — https://blog.statsbot.co/time-series-prediction-using-recurrent-neural-networks-lstms-807fa6ca7f
- Forecasting of Forex Time Series Data Based on Deep Learning — https://www.sciencedirect.com/science/article/pii/S1877050919302066
- How to Develop LSTM Models for Time Series Forecasting — https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/
- Multivariate Time Series Forecasting with LSTMs in Keras — https://machinelearningmastery.com/multivariate-time-series-forecasting-lstms-keras/