Автоматическая сегментация изображений (image segmentation) — востребованное направление использования нейронных сетей. Например, чтобы вручную разметить спутниковые снимки, обрисовав контуры домов, дорог, парковых зон и пр., нужно потратить колоссальное количество времени. Разметка клеток на фото с микроскопа в медицинских исследованиях тоже то ещё развлечение для фрилансеров. 🙂 В общем, приложений — множество.
Этот труд довольно простой, не требует высокой квалификации, трудоемкий и относительно недорогой. Например, простая сегментация одного изображения самолета стоит порядка 18 руб. за одну картинку в специализированной компании.
Очевидно, что подобную рутинную задачу хотелось бы переложить на «плечи» подходящей нейронной сети. Подать ей на вход обучающую выборку в которую войдут исходное изображение и сегментированное и получить модель, которая сможет выполнять автоматическую разметку в дальнейшем.
Разрешение исходного изображения и сегментированного должны совпадать. При использовании методов augmentation меняющих геометрическую форму или положение в пространстве: поворот (rotation), масштабирование (scale), зеркалирование (H/V flip), обрезание (crop) — одно и то-же преобразование должно применяться как к исходному изображению, так и к описывающему его сегменту. Расхождений быть не должно, иначе это может повлиять на качество обучения нейронной сети.
Например, массив изображений самолетов в небе и массив соотвествующих им сегментированных изображений.
fig = plt.figure(figsize=(20,10))
a = fig.add_subplot(1, 2, 1)
imgplot = plt.imshow(images[index].convert('RGBA'))
a.set_title('Самолет')
a = fig.add_subplot(1, 2, 2)
imgplot = plt.imshow(segments[index].convert('RGBA'))
a.set_title('Сегментация')
Меры схожести при сегментировании
При тренировке нейронки ей нужно дать критерий того, насколько сгенерированное ею сегментирование для исходного изображения совпадает с сегментированием, выполненным человеком.
В качестве такого критерия используется два основных коэффициента:
Коэффициент Жаккара предложен П. Жаккаром (Jaccard) в 1901 г. :
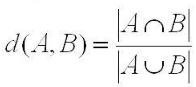
В числителе дроби стоит пересечение (intersection) множеств, а в знаменателе — общее количество элементов двух множеств (объединение или union).
def jaccard(a, b):
c = a.intersection(b)
return float(len(c)) / (len(a) + len(b) - len(c))
list1 = ['dog', 'cat', 'rat', 'elephant']
list2 = ['dog', 'cat', 'mouse', 'lion', 'panda']
# The intersection is ['dog', 'cat']
# The union is ['dog', 'cat', 'rat', 'mouse', 'elephant', 'lion', 'panda']
words1 = set(list1)
words2 = set(list2)
jaccard(words1, words2)
0.2857142857142857Или другой вариант кода на Python:
def jaccard(a, b):
c = a.intersection(b)
print("Intersection:", c)
print("Union:", a.union(b))
return len(c) / len(a.union(b)) Intersection: {'dog', 'cat'}
Union: {'panda', 'dog', 'mouse', 'cat', 'elephant', 'lion', 'rat'}В случае с сегментированным изображением внутри границы сегмента биты равны 1, а снаружи — 0. Соответственно, чтобы получить количество элементов в пересечении множеств, достаточно перемножить значения массива A на значения массива B. Или произвести более быструю операцию логического AND.
Там, где сегмент, отрисованный человеком, совпадает с предсказанными нейронкой, произведение 1 * 1 = 1. Если же нейронка неверно предсказала, то 1 * 0 = 0. В случае с numpy.array:
intersection = np.logical_and(a, b)
Коэффициент Дайса предложен Л.Дайсом в 1945 году, а для бинарной меры сходства используется коэффициент Сёренсена, предложенный Торвальдом Сёренсеном в 1948 году:
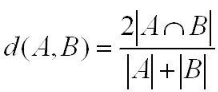
Поскольку в знаменателе фигурирует сумма количества элементов в каждом множестве без вычитания объединения множеств, то в числителе пересечение умножается на 2. Т.е. если множества пересеклись полностью, то |A| = |B| = |A ∩ B| и коэффициент Дайса даст 1.
def dice(a, b): c = a.intersection(b) return (2. * len(c)) / (len(a) + len(b))
Jaccard: 0.2857142857142857 Dice: 0.4444444444444444
Чтобы при нулевых длинах множеств A и В не получилось деления на 0, в числителе и знаменателе иногда добавляют по 1.
Функция Дайса, которую можно использовать в качестве loss и метрики:
# Функция, которая смотрит на пересечение областей. Нужна для accuracy
def dice_coef(y_true, y_pred):
return (2. * K.sum(y_true * y_pred) + 1.) / (K.sum(y_true) + K.sum(y_pred) + 1.)Подготовка изображения для сегментирования
Изображения контурятся, например, в графическом редакторе с помощью инструмента «Magic Wand» руками фрилансеров. Рассмотрим внимательнее, что получается на выходе. Я загрузил в массив images[] исходные изображения, а в segments[] — подготовленные фрилансерами сегменты.
Чтобы разбить исходное изображение по слоям R,G,B можно воспользоваться стандартным механизмом numpy.array:
r, g, b = image[:, :, 0], image[:, :, 1], image[:, :, 2] # For RGB image r, g, b = image[:, :, 0], image[:, :, 1], image[:, :, 2], image[:, :, 3] # for BGRA image
- 0 index value for Red channel
- 1 index value for Green channel
- 2 index value for Blue channel
Т.е. берутся все значения из каждого слоя. Того же результата можно добиться, используя dsplit:
r, g, b = np.dsplit(np.array(images[0]),np.array(images[0]).shape[-1])
Разобьем сегментирование по слоям, чтобы понять, как выглядит результат работы фрилансеров:
colors = ['Red', 'Green', 'Blue'] fig = plt.figure(figsize=(20,10)) for i in range(1, 4): a = fig.add_subplot(1, 3, i) pic = np.array(segments[0]) split_img = np.zeros(pic.shape, dtype="uint8") split_img[ :, :, i - 1] = pic[ :, :, i - 1] imgplot = plt.imshow(split_img) a.set_title(colors[i-1])

Если посмотреть статистику по цветам в слое Red (0-м), то видно, что там присутсвует не только красный и черный, но есть и градации цветов, причем они есть и в Green, Blue слоях.
imageForTest = segments[0]
r, g, b = np.dsplit(np.array(imageForTest ),np.array(imageForTest ).shape[-1])
unique, counts = np.unique(r, return_counts=True)
print("Unique:", unique)
print("Counts:", counts)Counts: [111814 385 74 238 208 66 365 129 79 45
37 36 19 27 23 14 9 15 20 10
12 14 13 12 9 10 16 9 6 9
...
8 12 16 7 19 12 10 17 15 21
24 28 36 35 44 43 77 93 107 74
173 178 152 387 12708 203]Для визуализации построим гистограмму от логарифма количества повторений цветов:
plt.figure(figsize=(10,5)) plt.bar(unique, np.log(counts)) plt.show()
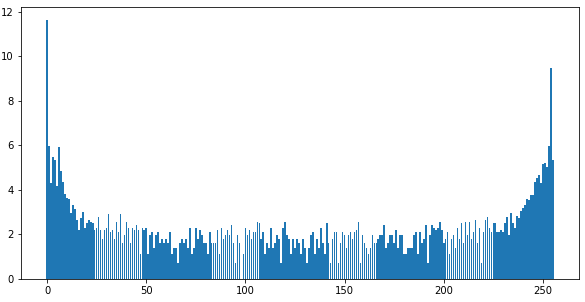
Как видно, основные цвета — черный и красный + градации. Градации при сегментировании, вроде как, не нужны (нужно проверять), уберем их, заменив все цвета с цифрами меньше 200 на черные (0), а все, что выше, — на 254:
def imageToOHE(image):
pic = np.array(image)
res = np.zeros(pic.shape)
for x in range(pic.shape[0]):
for y in range(pic.shape[1]):
if (pic[x, y, 0] > 200):
res[x, y, 0] = 254
return res
new_img = imageToOHE(imageForTest)
fig = plt.figure(figsize=(20,10))
a = fig.add_subplot(2, 1, 1)
imgplot = plt.imshow(imageForTest.convert('RGBA'))
a.set_title('Оригинальное')
a = fig.add_subplot(2, 1, 2)
imgplot = plt.imshow(new_img)
a.set_title('Новое')
unique, counts = np.unique(np.array(new_img), return_counts=True)
print("Unique:", unique)
print("Counts:", counts)
Без градаций изображение более «щербатое», но в данном случае не очень принципиально.
Циклы в Python работают чудовищно медленно. Нужно по возможности их избегать, используя нативные методы Python. Например, функция imageToOHE может быть записана короче на родных функциях Python:
def imageToOHE(image): pic = np.array(image) pic[pic<200] = 0 pic[pic>199] = 254 return pic
Вместо 254 при подготовке данных для нейронной сети нужно будет поставить 1, чтобы utils.to_categorical() корректно перевела в два класса. 254 задано, чтобы визуально можно было посмотреть, как отработал алгоритм преобразования.
Мне сходу не удалось просто на бинарных изображениях в одном слое сегментированного изображения получить нормальный результат. Только вариант с One Hot Encoding (OHE) выдал нормальный результат. Возможно, где-то ошибся с преобразованиями, либо надо в качестве loss использовать sparse_categorical_crossentropy.
Преобразование цветов сегмента в One Hot Encoding (OHE)
Классический вариант, рассказанный Дмитрием Романовым в «Университете искуственного интеллекта«, — это перевод разметки (сегментирования) в OHE. Учебный код Дмитрия:
# One hot encoding для 12 классов
def oneHot12(dSet): # dSet в нашем случае разметка
dSet12 = []
for t in range(dSet.shape[0]):
yy = dSet[t].copy()
yyNew = []
for i in range(yy.shape[0]):
currYYstr = []
for j in range(yy.shape[1]): # Цвет каждого пикселя
currYYstr.append(utils.to_categorical(yy[i][j][0], 12)) # представляем в виде вектора (12,)
yyNew.append(currYYstr)
yyNew = np.array(yyNew) # Список закодированных пикселей
dSet12.append(yyNew) # Список закодированных картинок
dSet12 = np.array(dSet12)
return dSet12Это пример, когда выполняется сегментирование на 12 классов для разметки дороги: дорожное покрытие, знаки, бордюр, тротуар, люди, машины, деревья и пр. Сегментированное фрилансерами изображение передается в варианте картинки, у которой в 0-м слое для каждого пикселя цифрами от 0 до 11 задан номер класса для сегментирования.
Соответственно, на функцию oneHot12 подается массив с размерностью оригинальных картинок, которые надо сегментировать, но с номерами размеченных классов вместо цвета пикселя.
Функция сначала перебирает по картинкам, а затем попиксельно просматривает картинку, переводя номер класса каждого пикселя в utils.to_categorical(yy[i][j][0], 12). В результате у картинки появляется размерность 12. Т.е., например, вместо картинки 240х480х3 (информация о классе в 0-м слое) с сегментированием появляется 240х480х12, где 12 — это categorical.
По сути это визуально можно представить в виде 12 слоев исходного изображения, в каждом из которых стоит 0 или 1 в соответствии с бинарной последовательностью, полученной после utils.to_categorical(yy[i][j][0], 12).
В дальнейшем станет понятнее, когда я разберу пример сегментирования самолета в небе. В этой задаче всего два класса, поскольку картинка бинарная: либо красный цвет сегмента, либо черный цвет фона.
Для начала рассмотрю интуитивно понятный вариант перевода сегментированного изображения в категории. Для удобства разобью исходную функцию Дмитрия на две: одна выполняет преобразование одной сегментированной картинки в изображение с категориями, а вторая передает на вход первой функции картинки для преобразования всей выборки.
def imageToCategorical(img, class_num):
new_img = []
img = imageToOHE(img)
for x in range(img.shape[0]):
currImgRow = []
for y in range(img.shape[1]): # Цвет каждого пикселя
currImgRow.append(utils.to_categorical(img[x][y][0], class_num)) # представляем в виде вектора (clas_num,)
new_img.append(currImgRow)
return np.array(new_img) # Список закодированных пикселейЗдесь все так же, как в коде Дмитрия, но добавлена функция imageToOHE для преобразования картинки с большим количеством цветов в бинарную, где лишние цвета обрезаны и остались только черный и красный (заменен на 1). Количество классов будет 2: черный фон и изображение сегмента.
Все просто, но работает очень долго, поэтому такой вариант не очень хорош, с учетом, что в процессе иследования Colab периодически дисконнектится, и нужно повторять преобразование исходных изображений сегментов в categorical. После некоторых экспериментов я нашел на порядки более быстрый вариант, когда преобразование 700 картинок 280х 160 занимает буквально секунду вместо нескольких минут циклами.
#Преобразование изображения в categorical def imageOHE(image, class_num, black_color = 200): pic = np.array(image) img = np.zeros((pic.shape[0], pic.shape[1], class_num)) np.place(img[ :, :, 0], pic[ :, :, 0] < black_color, 1) #utils.to_categorical(0, class_num).astype(np.uint8)) np.place(img[ :, :, 1], pic[ :, :, 0] < black_color, 0) np.place(img[ :, :, 0], pic[ :, :, 0] >= black_color, 0) #utils.to_categorical(1, class_num).astype(np.uint8)) np.place(img[ :, :, 1], pic[ :, :, 0] >= black_color, 1) return img img = imageOHE(segments[0], 2) print(img.shape)
В аргументе передается:
- Изображение с сегментом с градациями, оставленными фрилансерами,
- Количество классов. По большому счету в данном примере этот параметр не требуется, поскольку только два жестко заданных класса.
- Граница цвета пикселей, ниже которой цвета относятся к черному, а выше — к красному.
Первым делом формируется «чистое» изображение с 0-ми во всех слоях классов: np.zeros((pic.shape[0], pic.shape[1], class_num)).
Затем с помощью np.place все пиксели в 0-м и первом слое заменяются на categorical: все, что меньше black_color, на[1, 0], а все, что больше или равно, на [0, 1]. В данном случае я захардкодил два слоя, соответствующие классам. Можно было сначала взять utils.to_categorical(pixel_color, class_num).astype(np.uint8)) и в цикле пройтись по всем слоям, подставляя в каждый слой соответствующий бит, полученный после utils.to_categorical. Но в данном случае проще так.
В результате работы функции в двух слоях изображения закодирован нужный categorical.
Ну и простая часть — это перебор по всем картинкам и «скармливание» функции imageOHE:
# One hot encoding для 3 классов
def fastOHE(images, class_num):# dSet в нашем случае разметка
newImages = []
for t in range(images.shape[0]):
img = images[t].copy()
new_img = imageOHE(img, class_num, black_color = 200)
newImages.append(new_img) # Список закодированных картинок
newImages = np.array(newImages)
return newImagesВосстановление сегмента после предсказания нейронной сетью
На выходе нейронной сети, как итог предсказания по исходному изображению, будет матрица картинки с двумя размерностями, соответствующими categorical.
pred = model.predict(xTest) print(pred.shape) (140, 160, 280, 2)
Но вместо 0 и 1 будут некоторые вероятности, т.е. цифры в диапазоне от 0 до 1. Для преобразования в число из categorical из вектора берется номер наибольшей вероятности. Например, получили вектор [0.887788, 0.178567], np.argmax определит, что нейронка предсказала, что с вероятностью 0.88 пиксель должен быть черным, т.е. с порядковым номером 0.
В учебном коде Дмитрия подобное обратное преобразование выполняется следующим образом:
# Функция, перекрашивающая в один из 3 основных цветов
def color3(dSet): # dSet в нашем случае разметка
out3 = []
for pr in dSet:# проходимся по загруженной выборки
currPr = pr.copy() # делаем копию выборки
currMatr = []
for i in range(currPr.shape[0]): # проходимся по картинке
currStr = []
for j in range(currPr.shape[1]):
currStr.append(index2Color(np.argmax(currPr[i][j]))) # в наш выход добавляем преобразованный пиксель определенной картинки,
# но цветовое решение здесь берется, исходя из максимального значения одного из трех главных цветов
currMatr.append(currStr) # список трансформированных картинок
out3.append(currMatr)
out3 = np.array(out3)
out3 = out3.astype('uint8') # Нормализация пикселей в диапазоне 0..255 (RGB)
return out3Функция делает следующее:
- Последовательно скользит по двухмерной матрице строк (оси X) и колонок (оси Y), выбирая по одному элементу. На рисунке я выделил правый верхний.
- Каждый элемент этой матрицы представляет собой вектор OHE с размерностью, равной количеству классов. На рисунке 5 слоев «изображения», пронумерованные от 1 до 5, соответствующие 5 классам. Я пронумеровал от 1, так привычнее, но в Python всё считается от 0.
- Этот вектор OHE при исходном кодировании функцией oneHot12(dSet) был создан функцией utils.to_categorical().
- В этом, изначально разреженном, векторе (до подачи его на нейронку), закодирован номер класса. Вектор был преимущественно заполнен 0-ми. Порядковый номер, где стоит 1, соответствует номеру класса. На рисунке указан вектор OHE: [0, 0, 0 , 1, 0], соответствующий номеру класса 4 (считаем от 1).
- После обучения нейронки она предсказывает не 0 и 1, а вероятности, т.е. цифры в диапазоне 0..1. Вектор уже не разреженный.
- Если использовать np.argmax() над этим вектором OHE, то функция выберет максимальное значение среди чисел в векторе и возьмет его порядковый номер. Он будет соответствовать номеру класса. Например, нейронка предсказала, что крайний правый элемент матрицы: [0.01, 0.05, 0.07, 0.76, 0.03].
np.argmax( [0.01, 0.05, 0.07, 0.76, 0.03] ) = 3 (считается от 0).
Я переписал этот учебный код на существенно более быстрый вариант:
#Обратное преобразование из categorical в бинарное изображение и затем раскраска
def predToImage(segment):
img = np.zeros((segment.shape[0], segment.shape[1], 3))
img[:, :, 0] = (np.argmax(segment, axis=2)*254)
return img.astype('uint8')- Сначала создается «чистое» черное RGB изображение.
- С помощью np.argmax(segment, axis=2) по третьей оси (на рисунке обозначенной как OHE) из массива segment берется вектор OHE. Как уже говорилось ранее, в этом векторе после предсказания нейронкой уже не 0 и 1, а вероятности в диапазоне [0, 1].
- Полученный номер класса приводится к виду, который можно визуализировать, умножением на 254. Соответственно, в примере с сегментированием самолетов только два класса. 1-й класс соответствует красному цвету.
- Полученный слой записывается в 0-й (Red) слой «чистого» изображения: img[:, :, 0].
- На выходе обязательно нужно привести матрицу к img.astype(‘uint8’), чтобы не возникало ошибки, поскольку в изображении могут быть только целочисленные значения 0..254.
Этот код отрабатывает на тестовых картинках практически мгновенно. Чтобы увидеть предсказанную сегментацию в градациях серого нужно:
- Умножить полученные вероятности в 1-м слое, соответствующем красному цвету, на 254, чтобы привести в диапазон градаций красного [0..254].
- Скопировать полученное скорректированное изображение во все три слоя RGB, чтобы при смешении цветов получились градации серого.
- Сделать приведение img.astype(‘uint8’), чтобы не появлялась ошибка.
#Обратное преобразование из categorical в grayscale изображение, чтобы посмотреть детали сегментации
def predToGrayImage(segment):
img = np.zeros((segment.shape[0], segment.shape[1], 3))
img[:, :, 0] = segment[:, :, 1]*254
img[:, :, 1] = img[:, :, 0] #Make greyscale
img[:, :, 2] = img[:, :, 0] #Make greyscale
return img.astype('uint8') Для визуализации полученных изображений нужно пройтись в цикле по всем восстановленным после предсказания нейронкой картинкам и отобразить их:
def fastPrintPrediction(segments, images, num_to_show):
fig = plt.figure(figsize=(20, 10)) # указываем размеры фигуры
columns = 3
rows = num_to_show #len(arr_img)
index = 1
plt.figure(figsize=(6*columns, 4*rows)) # указываем размеры фигуры
for i in range(rows): #
ax = plt.subplot(rows, columns, index)
ax.set(title = i)
index += 1
plt.imshow(images[i].convert('RGBA')) #Show the source image
ax = plt.subplot(rows, columns, index)
ax.set(title = i)
index += 1
segment = predToImage(segments[i])
plt.imshow(segment) #Show the image segment
ax = plt.subplot(rows, columns, index)
ax.set(title = i)
index += 1
grayed_segment = predToGrayImage(segments[i])
plt.imshow(grayed_segment) #Show the image grayscale segment
plt.show()Результат предсказания сегментов нейронной сетью:


Если изображение не очень контрастное, или фон сливается с цветом самолета, то нейронка не четко «вытягивает» его контуры. Например, если самолет на фоне облаков, то они дают шумовой эффект, размазывая границы сегмента. В данном случае можно добавить augmentation при обучении сети.
Кроме того, исходное изображение можно дополнительно преобразовать, повысив контраст, инвертировав и пр. Аугментированные изображения можно подать на нейронку совместно с исходным. Естественно, все подобные операции над изображениями увеличат время обучения нейронной сети.
Наш куратор на курсе обучения в университете Герард сказал, что: «Границы хорошо отрабатывает использование dice coefficient в качестве loss».
Приницип работы U-net для сегментирования
Архитектура UNET взята классическая из учебного курса Дмитрия Романова. Она же фигурирует в массе статей из списка литературы в конце.
Смысл в том, что исходное изображение преобразуется сверточными слоями Conv2D. Картинка немного неточная, поскольку в современных реализациях у сверточного слоя задается padding=’same’. При этом параметре размерность изображений, выдаваемых на выходе каждого горизонтального (на рисунке) сверточного слоя, остается неизменной. На рисунке же из-за strides = (2, 2) разрешение после каждого горизонтального сверточного слоя уменьшается на 2.
После серии сверточных слоев в пределах горизонтального уровня идет «бутерброд» из слоев нормализации (BatchNormalization) и активационного (его можно вынести в аргумент Conv2D, убрав слой).
После этого «бутерброда» стоит слой MaxPooling2D, который уменьшает разрешение (размерность) исходного изображения вдвое (в примере учебного кода ниже). При таком коде размерность должна быть кратна двум (чётное число). При каждом делении на 2 размерность изображения должна оставаться чётной. Например, в примере кода три слоя MaxPooling2D (один закомментирован, поскольку разрешение изображения низкое), т.е. нужно, чтобы можно было исходное разрешение по всем осям делить нацело на 2, причем три раза подряд.
Если деление разрешения на 2 будет не нацело, то появится нечетное число в разрешении. При обратной операции удвоения разрешения изображений слоями Conv2DTranspose такие нечетные числа приведут к тому, что разрешение изображения на одной линии преобразования слева и справа будут разными и конкатенация concatenate() выдаст ошибку.
Можно просто обрезать (кропать/crop) нечетное изображение, чтобы при восстановлении конкатенация была успешной, независимо от размерности исходной картинки. Для этих целей в Keras есть слой Cropping2D(), обрезающий исходное изображение до нужного без мороки с подбором разрешений, кратных двойке.
На каждом шаге понижения размерности нейронка переходит от более мелких деталей к все более крупным, каждый раз выполняя смешивание изображений с разными уровнями детализации для обработки сверточным слоем.
В человеческом представлении нейронка смотрит на один и тот же объект с разных расстояний: вблизи нейронка «рассматривает» очень мелкие детали, по которым нельзя понять, что это за объект, поэтому она как бы «удаляется», чтобы «увидеть» объект целиком.
Анализ первого уровня детализации изображения (попиксельный) — это все равно, что рассматривать фото кристалла сахара в микроскопе и пытаться понять геометрическую форму кусочка сахара-рафинада, который из них состоит. 🙂 Сравнение, конечно, очень условное.
Пример кода U-net для сегментирования картинок
Исходные картинки преобразуются в массив numpy array.
#преобразуем каждую из картинок в массив (высота, ширина, количество каналов)
def prepareTrainImages(trainIm):
xTrain = []
for img in trainIm:
x = image.img_to_array(img)
xTrain.append(x)
xTrain = np.array(xTrain)
return xTrainЗатем порядка 20% от исходной выборки берется на проверочную:
x_size = 160 #280 #Пропорциональное изменение картинки y_size = 280 #480 num_of_train = 700 num_of_test = int(np.floor(num_of_train*0.2))
И выполняется разделение на xTrain, xTest.
#преобразуем каждую из картинок в массив (высота, ширина, количество каналов) xTrain = prepareTrainImages(images[:num_of_train]) _xTest = images[num_of_train:num_of_train+num_of_test] xTest = prepareTrainImages(_xTest)
и то же для yTrain, yTest.
# аналалогично для карт сегментации yTrain = prepareTrainImages(segments[:num_of_train]) yTest = prepareTrainImages(segments[num_of_train:num_of_train+num_of_test])
Перед подачей данных на нейронку для Y картинки с сегментацией преобразуются в categorical на 2 класса:
# Производим one hot encoding на 3 yTrain3 = fastOHE(yTrain, 2) yTest3 = fastOHE(yTest, 2) print(yTrain3.shape) print(yTest3.shape) (700, 160, 280, 2) (140, 160, 280, 2)
Добавление разреженных (sparse) слоев, забитых 0 и 1, отъедает памяти GPU/TPU. Можно попробовать обойтись без этого преобразования, использовав в качестве loss — sparse_categorical_crossentropy вместо categorical_crossentropy. Пишите, какие будут результаты.
С Unet основная проблема, что разрешение входной картинки должно быть подобрано таким образом, чтобы оно нацело делилось на каждом этапе понижения размерности. В противном случае конкатенация не будет отрабатывать, поскольку разрешение на слоях восстановления будет на 1 отличаться от соответствующего понижающего слоя. Как сказал Дмитрий, для решения можно использовать следующие подходы:
- кропить картинку до размера, кратного степени 2, и обучать на кропах
- менять размер через conv2d и conv2dtranspose, убрав padding=same, можно делать размеры +2 и -2 при ядре 3,3 или +4 и -4 при ядре 5,5 и т.п.
- не использовать unet и pspnet, использовать просто разные ядра свёртки с конкатинацией — от 2 до 64 или даже 128, это тоже неплохо работает
def unet(num_classes = 2, input_shape= (x_size, y_size, 3)):
img_input = Input(input_shape)
# Block 1
x = Conv2D(64, (3, 3), padding='same', name='block1_conv1')(img_input)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(64, (3, 3), padding='same', name='block1_conv2')(x)
x = BatchNormalization()(x)
block_1_out = Activation('relu')(x)
x = MaxPooling2D()(block_1_out)
# Block 2
x = Conv2D(128, (3, 3), padding='same', name='block2_conv1')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(128, (3, 3), padding='same', name='block2_conv2')(x)
x = BatchNormalization()(x)
block_2_out = Activation('relu')(x)
x = MaxPooling2D()(block_2_out)
# Block 3
x = Conv2D(256, (3, 3), padding='same', name='block3_conv1')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (3, 3), padding='same', name='block3_conv2')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (3, 3), padding='same', name='block3_conv3')(x)
x = BatchNormalization()(x)
block_3_out = Activation('relu')(x)
x = MaxPooling2D()(block_3_out)
# Block 4
x = Conv2D(512, (3, 3), padding='same', name='block4_conv1')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(512, (3, 3), padding='same', name='block4_conv2')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(512, (3, 3), padding='same', name='block4_conv3')(x)
x = BatchNormalization()(x)
block_4_out = Activation('relu')(x)
#x = MaxPooling2D()(block_4_out)
# Block 5
#x = Conv2D(512, (3, 3), padding='same', name='block5_conv1')(x)
#x = BatchNormalization()(x)
#x = Activation('relu')(x)
#x = Conv2D(512, (3, 3), padding='same', name='block5_conv2')(x)
#x = BatchNormalization()(x)
#x = Activation('relu')(x)
#x = Conv2D(512, (3, 3), padding='same', name='block5_conv3')(x)
#x = BatchNormalization()(x)
#x = Activation('relu')(x)
#Load pretrained weights.
#for_pretrained_weight = MaxPooling2D()(x)
#vgg16 = Model(img_input, for_pretrained_weight)
#vgg16.load_weights('vgg16_weights_tf_dim_ordering_tf_kernels_notop.h5', by_name=True)
# UP 1
#x = Conv2DTranspose(512, (2, 2), strides=(2, 2), padding='same')(x)
#x = BatchNormalization()(x)
#x = Activation('relu')(x)
#x = concatenate([x, block_4_out])
#x = Conv2D(512, (3, 3), padding='same')(x)
#x = BatchNormalization()(x)
#x = Activation('relu')(x)
#x = Conv2D(512, (3, 3), padding='same')(x)
#x = BatchNormalization()(x)
#x = Activation('relu')(x)
# UP 2
x = Conv2DTranspose(256, (2, 2), strides=(2, 2), padding='same', name = 'Conv2DTranspose_UP2')(block_4_out)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = concatenate([x, block_3_out])
x = Conv2D(256, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
# UP 3
x = Conv2DTranspose(128, (2, 2), strides=(2, 2), padding='same', name = 'Conv2DTranspose_UP3')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = concatenate([x, block_2_out])
x = Conv2D(128, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(128, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
# UP 4
x = Conv2DTranspose(64, (2, 2), strides=(2, 2), padding='same', name = 'Conv2DTranspose_UP4')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = concatenate([x, block_1_out])
x = Conv2D(64, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(64, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(num_classes, (3, 3), activation='sigmoid', padding='same')(x)
model = Model(img_input, x)
model.compile(optimizer=Adam(lr=0.005),
loss='categorical_crossentropy',
metrics=[dice_coef])
model.summary()
return modelПолезные ссылки
- https://www.codementor.io/@innat_2k14/image-data-analysis-using-numpy-opencv-part-1-kfadbafx6
- Practical image segmentation with Unet. Русский перевод — «Задачи сегментации изображения с помощью нейронной сети Unet» —
- Небольшое исследование свойств простой U-net, классической сверточной сети для сегментации — https://habr.com/ru/company/ods/blog/431512/
- https://medium.com/beyondminds/a-simple-guide-to-semantic-segmentation-effcf83e7e54

